Jak tworzyć wykresy pudełkowe
Sprawdź, do czego przydają się wykresy pudełkowe oraz naucz się je poprawnie tworzyć na przykładzie Pythona.
Dzisiaj porozmawiamy trochę o wykresach pudełkowych. Jest to znormalizowany sposób na wyświetlanie dystrybucji danych opartych na pięcio liczbowym podsumowaniu (“minimum”, pierwszy kwartyl (Q1), mediana, trzeci kwartyl (Q3), oraz “maximum”).
Może on pokazać wartości odstające, stwierdzić, czy Twoje dane są symetryczne, jak mocno są one pogrupowane oraz czy i jak są zniekształcone.
Co zawiera ten tutorial:
- Definicję wykresu pudełkowego
- Wyjaśnienie anatomii wykresu pudełkowego poprzez porównanie go z funkcją gęstości prawdopodobieństwa dla rozkładu normalnego
- Wyjaśnienie tego, jak tworzyć i interpretować wykresy pudełkowe w Pythonie
Kod wykorzystany do stworzenia wykresów jest dostępny na moim GitHubie. A teraz zaczynajmy!
Czym jest wykres pudełkowy?
W przypadku niektórych rozkładów czy zbiorów danych okazuje się, że potrzebujesz więcej informacji niż pomiarów tendencji centralnej (mediana, średnia i moda).
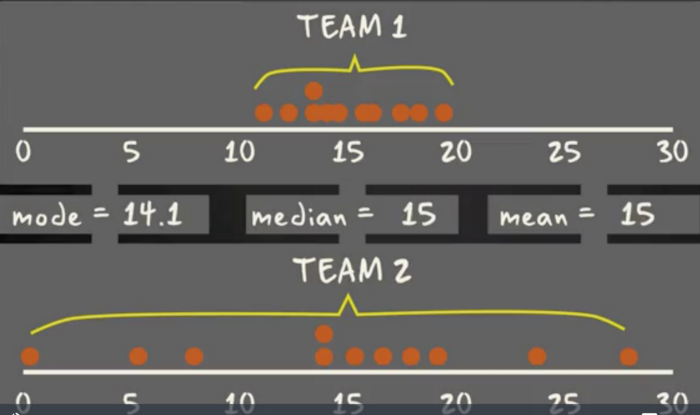 Są przypadki, w których średnia, mediana oraz moda nie są wystarczające, aby opisać zbiór danych (patrz tutaj).
Są przypadki, w których średnia, mediana oraz moda nie są wystarczające, aby opisać zbiór danych (patrz tutaj).
Potrzebujesz też informacji na temat różnorodności oraz dyspersji danych. Wykres pudełkowy daje Ci wgląd w to, jak wartości w danych się rozkładają.
Chociaż wykresy pudełkowe mogą wydawać się prymitywne w porównaniu z histogramami lub wykresami gęstości, to mają one tę zaletę, że zajmują mniej miejsca, co jest przydatne przy porównywaniu wielu grup lub zestawów danych.
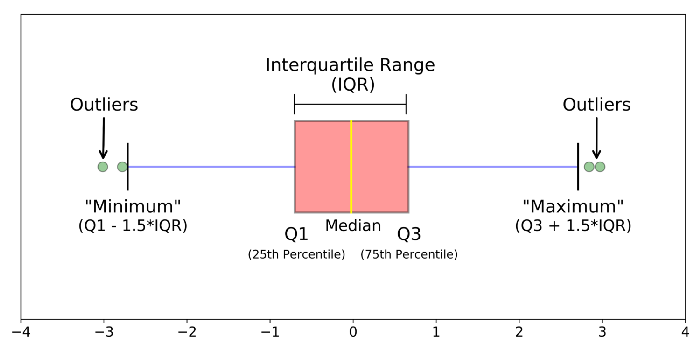
Różne części wykresu pudełkowego
mediana (Q2/percentyl 50): środkowa wartość zbioru danych.
pierwszy kwartyl (Q1/percentyl 25): środkowa liczba pomiędzy najmniejszą liczbą (nie „minimum”) a medianą zbioru danych.
trzeci kwartyl (Q3/percentyl 75): środkowa wartość między medianą a najwyższą wartością (nie „maksimum”) zbioru danych.
rozstęp ćwiartkowy (IQR): od percentyla 25 do 75.
“wąsy” wykresu (zaznaczone na niebiesko)
wartości odstające (zaznaczone w zielonych kółkach)
“maximum”: Q3 + 1.5*IQR
“minimum”: Q1 -1.5*IQR
To, co definiuje wartości odstające, „minimum” lub „maksimum”, może jeszcze nie być do końca jasne. W następnej sekcji postaramy się to lepiej wyjaśnić.
Wykres pudełkowy z normalnym rozkładem danych
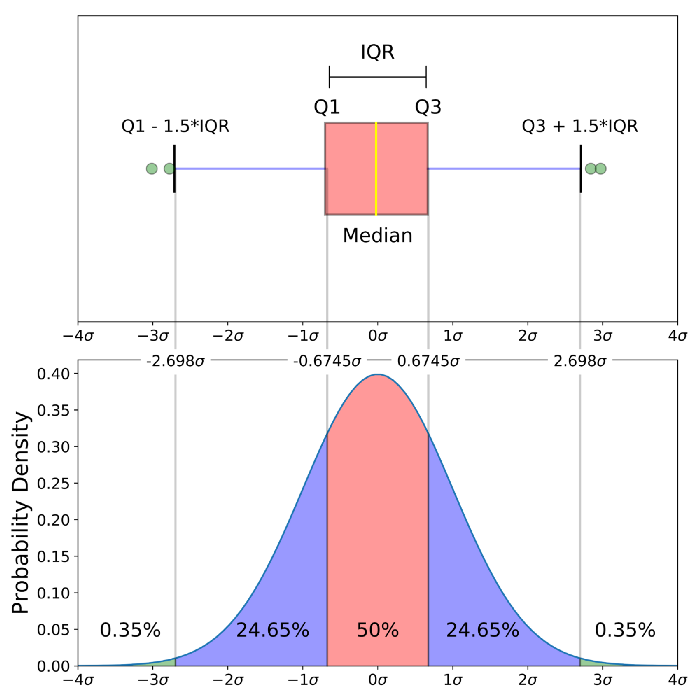
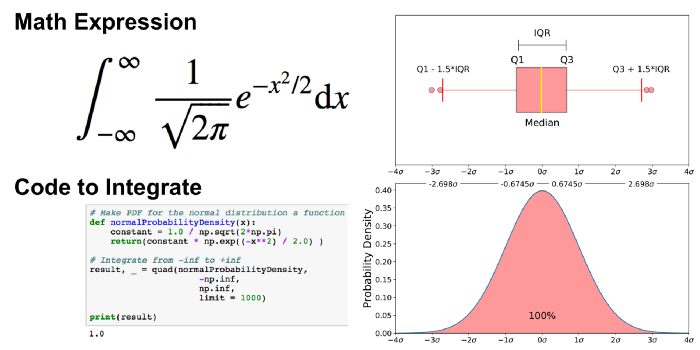
Porównanie wykresu pudełkowego o rozkładzie bliskim normalnemu i funkcji gęstości prawdopodobieństwa dla rozkładu normalnego
Pokazuję ten rysunek dlatego, że patrzenie na rozkład statystyczny jest bardziej powszechne niż patrzenie na wykres pudełkowy. Innymi słowy, może Ci to pomóc w zrozumieniu wykresu pudełkowego.
Sekcja ta obejmuje następujące rzeczy:
- Dlaczego wartości odstające stanowią (dla rozkładu normalnego) .7% danych.
- Co to jest „minimum” i „maximum”
Funkcja gęstości prawdopodobieństwa
Aby zrozumieć, skąd pochodzą procenty, ważne jest, aby rozumieć funkcję gęstości prawdopodobieństwa. Służy ona do określenia prawdopodobieństwa tego, że zmienna losowa mieści się w określonym zakresie wartości, w przeciwieństwie do przyjmowania dowolnej wartości.
Prawdopodobieństwo to jest określane przez całkę omawianej funkcji zmiennej w tym zakresie - jest to pole pod funkcją gęstości, ale powyżej osi poziomej i między najniższą a największą wartością zakresu.
Powyższe może być jeszcze niejasne. Stwórzmy zatem wykres funkcji gęstości prawdopodobieństwa dla rozkładu normalnego. Oto równanie:
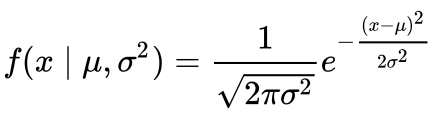
Uprośćmy, zakładając, że mamy średnią (μ) równą 0 i odchylenie standardowe (σ) równe 1.
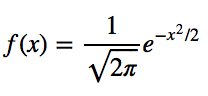
Ja stworzę wykres przy pomocy Pythona. Ty możesz w czym chcesz.
# Import all libraries for this portion of the blog post
from scipy.integrate import quad
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.linspace(-4, 4, num = 100)
constant = 1.0 / np.sqrt(2*np.pi)
pdf_normal_distribution = constant * np.exp((-x**2) / 2.0)
fig, ax = plt.subplots(figsize=(10, 5));
ax.plot(x, pdf_normal_distribution);
ax.set_ylim(0);
ax.set_title('Normal Distribution', size = 20);
ax.set_ylabel('Probability Density', size = 20);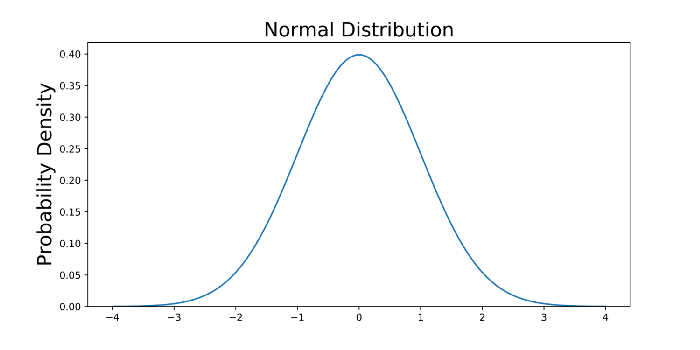
Powyższy wykres nie pokazuje prawdopodobieństwa zdarzeń, ale ich gęstość prawdopodobieństwa. Aby uzyskać prawdopodobieństwo zdarzenia w danym zakresie, będziemy musieli obliczyć całki.
Załóżmy, że chcemy znaleźć prawdopodobieństwo tego, że losowy punkt danych znajdzie się w przedziale międzykwartylowym równym .6745 odchylenia standardowego średniej, więc musimy całkować od -,6745 do 0,6745. Można to zrobić za pomocą SciPy.
# Make PDF for the normal distribution a function
def normalProbabilityDensity(x):
constant = 1.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) )
# Integrate PDF from -.6745 to .6745
result_50p, _ = quad(normalProbabilityDensity, -.6745, .6745, limit = 1000)
print(result_50p)To samo można zrobić dla „minimum” i „maximum”.
# Make a PDF for the normal distribution a function
def normalProbabilityDensity(x):
constant = 1.0 / np.sqrt(2*np.pi)
return(constant * np.exp((-x**2) / 2.0) )
# Integrate PDF from -2.698 to 2.698
result_99_3p, _ = quad(normalProbabilityDensity,
-2.698,
2.698,
limit = 1000)
print(result_99_3p)Jak wspomniano wcześniej, wartości odstające to pozostałe 0,7% danych.
Warto zauważyć, że dla każdej funkcji gęstości prawdopodobieństwa obszar pod krzywą musi wynosić 1 (prawdopodobieństwo wyciągnięcia dowolnej liczby z zakresu funkcji wynosi zawsze 1).
Rysowanie i interpretowanie wykresu pudełkowego
Darmowy podgląd z kursu pt. "Using Python for Data Visualization"
Sekcja ta jest w dużej mierze oparta na powyższym wideo z mojego kursu.
W ostatniej sekcji omówiliśmy wykres pudełkowy z rozkładem normalnym, ale ponieważ nie zawsze będziesz mieć do czynienia z rozkładem normalnym, to sprawdzimy, jak wykorzystać wykres pudełkowy na rzeczywistym zbiorze danych.
Wykorzystamy w tym celu zbiór danych ze strony Breast Cancer Wisconsin (Diagnostic). Jeśli nie masz konta Kaggle, możesz pobrać ten dataset z mojego GitHuba.
Czytanie danych
Poniższy kod sczytuje dane do pandas dataframe.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Put dataset on my github repo
df = pd.read_csv('https://raw.githubusercontent.com/mGalarnyk/Python_Tutorials/master/Kaggle/BreastCancerWisconsin/data/data.csv')
Wykres pudełkowy
Wykres pudełkowy służy nam do analizy związku między cechą jakościową (guz złośliwy lub łagodny) a cechą ciągłą (area_mean).
Istnieje kilka sposobów na nakreślenie wykresu pudełkowego w Pythonie. Możesz to zrobić m.in. za pomocą seaborn, matplotlib, czy pandas.
seaborn
Poniższy kod przekazuje pandas dataframe df do wykresu pudełkowego seaborn.
sns.boxplot(x='diagnosis', y='area_mean', data=df)matplotlib
Wykresy pudełkowe z tego artykułu zostały utworzone za pomocą matplotlib. Takie podejście może być bardziej żmudne, ale zapewnia też wyższy poziom kontroli.
malignant = df[df['diagnosis']=='M']['area_mean']
benign = df[df['diagnosis']=='B']['area_mean']
fig = plt.figure()
ax = fig.add_subplot(111)
ax.boxplot([malignant,benign], labels=['M', 'B'])Ale wystarczy trochę pracy i możemy mieć łatwiej.
pandas
Wykres pudełkowy można stworzyć, wywołując .boxplot() w DataFrame. Poniższy kod tworzy wykres pudełkowy kolumny area_mean w odniesieniu do różnych diagnoz.
df.boxplot(column = 'area_mean', by = 'diagnosis');
plt.title('')Zawężony wykres pudełkowy
Zawężony wykres pudełkowy umożliwia ocenę przedziałów ufności (domyślnie 95% przedział ufności) dla median każdego wykresu pudełkowego.
malignant = df[df['diagnosis']=='M']['area_mean']
benign = df[df['diagnosis']=='B']['area_mean']
fig = plt.figure()
ax = fig.add_subplot(111)
ax.boxplot([malignant,benign], notch = True, labels=['M', 'B']);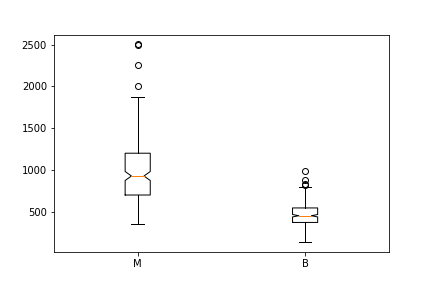
Jeszcze będziemy poprawiać
Interpretacja wykresu pudełkowego
Data science polega na czytelnym pokazywaniu danych, więc pamiętaj, że Twoje wykresy pudełkowe mogą zawsze być lepsze (kod tutaj).
Korzystając z wykresów możemy porównać zakres i rozkład area_mean dla diagnozy złośliwego lub łagodnego guza. Zauważamy, że istnieje większa zmienność dla średniej wielkości guza złośliwego, jak również dla większych wartości odstających.
Ponadto, ponieważ nacięcia na wykresach pudełkowych nie pokrywają się, to można stwierdzić, że rzeczywiste mediany będą się prawdopodobnie różnić.
Oto kilka innych rzeczy, o których należy pamiętać w przypadku wykresów pudełkowych:
- Pamiętaj, że zawsze możesz wyciągnąć dane z wykresu pudełkowego, aby dowiedzieć się, jakie są wartości liczbowe dla różnych jego części.
- Matplotlib nie zakłada, że ma do czynienia z rozkładem normalnym i nie wykorzystuje takiej estymacji do wyliczenia kwantyli. Mediana i kwartyle są obliczane bezpośrednio na podstawie danych. Innymi słowy, wykres pudełkowy może wyglądać inaczej w zależności od rozkładu danych i wielkości próby, np. asymetrycznie i z mniejszą lub większą liczbą wartości odstających.
Podsumowanie
Mam nadzieję, że nie zasypałem Was zbyt dużą ilością informacji oraz, że ten tutorial się Wam przyda.
Oryginał tekstu w języku angielskim przeczytasz tutaj.


