Czym jest logarytmiczna złożoność czasowa
Dowiedz się, czym jest logarytmiczna złożoność czasowa oraz poznaj cztery ważne kategorie notacji dużego O.
Jeśli rozpoczynasz swoją przygodę związaną ze światem IT, prawdopodobnie miałeś już okazję widzieć coś podobnego do: O(n) lub O(log n). To analiza złożoności czasowej lub tzw. notacja dużego O.
Bardzo ważne jest zrozumienie tej koncepcji, przynajmniej intuicyjnie, aby móc w przyszłości pisać szybki kod. Jest jeszcze coś takiego jak złożoność pamięciowa, która pokazuje, jak dużo pamięci może zużyć program, ale zostawmy to na następny artykuł.
To z powodu tej koncepcji na studiach programistycznych studenci katowani są godzinami matematyki. Co prawda nie mam nic przeciwko zajęciom z matematyki, ale naprawdę nie potrzebujesz ich, żeby pisać dobry kod.
W rzeczywistości wszystkie założenia informatyczne, które musi znać przeciętny programista, nie są trudne same w sobie. Podobnie jest z kodem - jego składowe nie są skomplikowane, ale łączą się w bardziej złożoną i wieloaspektową całość.
Czym jest n?
“Złożoność czasowa to złożoność obliczeniowa opisująca czas potrzebny do uruchomienia algorytmu.”
- tłumaczenie z angielskiej Wikipedii
To dość zawiłła definicja, więc uprośćmy ją.
Omówię cztery ważne kategorie notacji dużego O. Istnieją również inne, takie jak n log n i n silnia, ale na razie je pominiemy.
Powiedzmy, że mamy listę pięciu liter:
[a,b,c,d,e]
Ponieważ jest ich pięć, n będzie równe 5: n=5.
Czas stały lub O(1)
Jeśli Twój program chce usunąć jedną literę z listy w ten sposób:
[a,b,c,d,e] => [a,b,c,d]
Jego złożoność czasowa wynosi po prostu 1, ponieważ nie ma znaczenia, ile liter znajduje się na liście. Zawsze będzie miała miejsce tylko jedna operacja.
O(1) to najlepsza możliwa złożoność czasowa. Struktury danych, takie jak tablice mieszające, sprytnie wykorzystują algorytmy do wykonywania operacji o stałym czasie, co przyspiesza działanie programu.
Czas liniowy lub O(n)
Jeśli Twój program robi coś w stylu powielania wszystkich liter w ten sposób:
[a,b,c,d,e] => [aa,bb,cc,dd,ee]
Dla każdej litery powstaje litera zduplikowana. Program wykonuje pojedyncze czynności po kolei.
Można powiedzieć, że jego czas wykonania jest rzędu n, ponieważ liczba operacji, które musi wykonać, jest proporcjonalna do liczby liter na liście. Czy można wywnioskować z tego, jak szybko program będzie działać w praktyce? Nie do końca.
Twoje dane mogą być równie dobrze dwoma literami, ale też dwoma miliardami liter. Program może zostać uruchomiony na starym laptopie lub super komputerze i zająć bardzo różną ilość czasu.
Jeśli program powiela każdą liczbę trzy razy zamiast dwóch, nadal będzie to O(n), ponieważ nawet jeśli wykonuje on więcej operacji na element, to o ile więcej na element jest tu stałe.
O(n) to przyzwoita złożoność czasowa i często ciężko jej uniknąć.
O(n²)
Teraz załóżmy, że chcesz, aby Twój program dodawał do siebie wszystkie elementy z listy.
[a,b,c,d,e] => [abcde, bacde, cabde, dabce, eabcd]
Ponieważ dla każdego elementu listy musisz znowu przejść resztę elementów w liście, to liczba operacji, które musi wykonać program to liczba elementów (czyli n) razy liczba elementów (czyli w sumie n²).
Jeśli Twoja lista zawiera dwie litery, Twój program wykona cztery operacje. Jeśli lista zawiera cztery biliony liter, może nigdy nie zakończyć swojego działania!
O(n²) prawie nigdy nie jest akceptowalną złożonością czasową i zwykle można jej uniknąć za pomocą jakiegoś sprytnego algorytmu.
Czas logarytmiczny lub O(log n)
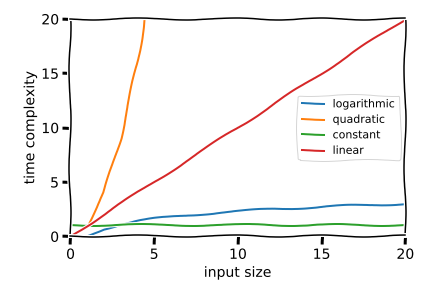
wykres matplotlib
Patrząc na ten rysunek, możesz zobaczyć, jak skaluje się każdy z czterech rodzajów złożoności czasowych.
Pomarańczowa linia rośnie bardzo szybko, podczas gdy zielona pozostaje na tym samy poziomie, bez względu na ilość elementów. A co z niebieską linią oznaczającą złożoność logarytmiczną? Zachowuje się prawie tak samo jak linia złożoności czasu stałego.
Logarytmy
Wielkość reprezentująca potęgę, do której należy podnieść stałą liczbę (podstawę), aby uzyskać daną liczbę. - tłumaczenie definicji z Lexico
Jeśli nie myślałeś o algebrze od czasów liceum, musisz przypomnieć sobie, czym do jasnej anielki jest logarytm.
Tako rzecze matematyka
Logarytmy służą do wyznaczania x, gdzie x to wykładnik potęgi. Spójrz na to równanie:
3^x == 9
Zapytanie, którego odpowiedzią będzie właśnie logarytm, brzmi: „Do jakiej potęgi podnieść 3, aby uzyskać 9?” Odpowiedź to oczywiście 2!
log3(9) == 2
Funkcja logarytmiczna jest przeciwieństwem funkcji wykładniczej. Kiedy mówisz, że coś rośnie wykładniczo, to znaczy, że się mnoży. Kiedy coś rośnie logarytmicznie, jest dzielone.
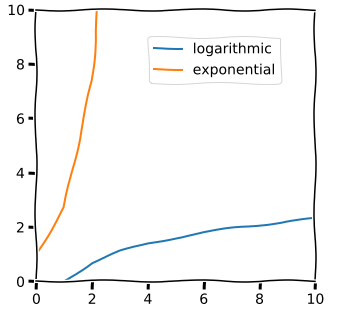
dwie przeciwne funkcje jak swoje lustrzane odbicia
Oznacza to, że jeśli masz dwa elementy listy do przerobienia(?), a program uruchamia się w czasie logarytmu dwójkowego, potrzeba jednej operacji na wykonanie tego. To naprawdę potężne działanie. Po uruchomieniu będzie mniej operacji, niż jest danych.
Im więcej danych wejściowych, tym proporcjonalnie mniej operacji program musi wykonać w porównaniu z ilością danych!
Logarytmy w praktyce
Spójrzmy ponownie na listę z początku artykułu:
[a,b,c,d,e]
Jeśli chcesz ją przeszukać i znaleźć np. element d, możesz napisać program, który prześledzi każdą literę po kolei i zwróci indeks (3) elementu, gdy go znajdzie.
To wyszukiwanie zajmie cztery operacje. Nie tak źle, prawda? A co by było, gdybyśmy zamiast tego szukali e? Tylko pięć operacji. Ponieważ jest to najgorszy scenariusz, a ilość danych wejściowych to 5, algorytmem wyszukiwania będzie O(n).
To dobre rozwiązanie w przypadku małej listy, ale gdybyśmy przeszukiwali listę z miliardem elementów, wykonywanie algorytmu zajęłoby dużo czasu.
Szukanie na przykładzie flamenco
A co by było, gdybyśmy mogli przyspieszyć to do O(log n). Jeśli lista jest posortowana, możemy to zrobić! Tancerze flamenco najlepiej to wytłumaczą:
Zwróć uwagę, że tancerze ustawiają się w jednej linii z numerami na plecach. Mężczyzna z numerem siedem szuka pasującej kobiety. Nie wie, gdzie ona jest, ale wie, że wszystkie panie są posortowane (jakkolwiek dziwnie to nie brzmi).
Jego proces polega na podejściu do tancerki pośrodku i zapytaniu, po której stronie ma panią z numerem siedem. Kiedy mówi: „Ona jest po mojej lewej stronie”, tancerz może wykluczyć wszystkich po jej prawej stronie.
Następnie zadaje to samo pytanie kobiecie znajdującej się pośrodku lewej strony. To pozwala mu wykluczyć drugą połowę kandydatów i tak dalej, aż znajdzie numer siedem.
Ten program działa w czasie O(log n), ponieważ w najgorszym przypadku liczba operacji potrzebnych do wykonania będzie logarytmem dwójkowym z wielkości wejścia. W tym przypadku, ponieważ na naszej „liście” jest siedmiu tancerzy, czas wykonywania wynosi log2(7) lub ~3 operacje.
Algorytm ten nazywa się wyszukiwaniem binarnym, ponieważ zawężasz wyszukiwanie o dwa przy każdej operacji. To idealny przykład dla O(log n).


