Trenuj lepsze modele Uczenia Maszynowego za pomocą Hyperopt

1. Czym są hiperparametry w modelach oraz dlaczego chcemy je optymalizować

Wiele najnowocześniejszych modeli uczenia maszynowego (ang. Machine Learning, ML) wymaga ogromnej ilości czasu na wytrenowanie z danych. Jednocześnie, te same algorytmy zawierają zwykle dziesiątki parametrów, które muszą być skonfigurowane przed treningiem. Takie zmienne konfiguracyjne modeli ML nazywane są hiperparametrami. Przykładem hiperparametrów w modelu SVM są: siła regularyzacji (często C), funkcja jądra oraz wewnętrzne hiperparametry jądra. Często hiperparametry mają znaczący wpływ na sukces algorytmu uczenia maszynowego.

Słabo skonfigurowana SVM może działać nie lepiej niż funkcja losowa, podczas gdy dobrze skonfigurowany może osiągnąć znakomitą dokładność predykcji. Nawet dla ekspertów dziedziny dostosowanie hiperparametrów może być zadaniem trudnym, żmudnym oraz czasochłonnym, a czasami wręcz niemożliwym.

2. Ogólne spojrzenie na problem optymalizacji modelu uczenia maszynowego

Czy hiperparametry SVM to wszystko, co można zoptymalizować? Nie do końca. A dlaczego został wybrany SVM? Często badacze wybierają model uczenia maszynowego opierając się o doświadczenie, gust lub obecne trendy. Dla jednego pierwszym modelem do spróbowania będzie regresja liniowa, dla innego Random Forest lub jedna ze znanych implementacji Gradient Boosting. Ale kto ma rację, jaki model da najlepsze wyniki? Odpowiedź na te pytania jest nieznana, aż wszystkie podejścia nie zostaną sprawdzone. A więc wychodzi na to, że sam wybór modelu też jest parametrem do optymalizacji.

Kluczowy wpływ na skuteczność modelu mają dane treningowe. Przygotowanie danych często jest pierwszym etapem analiz, gdzie już są podejmowane kluczowe decyzje, co będą miały wpływ na wynik końcowy. Czy stosować PCA z progiem 90%, może zmienić reprezentacje klas w problemie klasyfikacji za pomocą oversamplingu lub zlogarytmizować ciągłą zmienną oczekiwaną? Odpowiedź jest identyczna do poprzedniej – z góry tego nie znano. Decyzje co do przygotowania danych również mogą być optymalizowane.

Znalezienie optymalnego modelu to spróbowanie wszystkich możliwości przygotowania danych dla wszystkich modeli uczenia maszynowego dla wszystkich wartości hiperparametrów każdego modelu. Brzmi banalnie. Ale niestety spróbowanie wszystkich kombinacji jest niemożliwe, ze względu na czas obliczeń. Częstym podejściem jest użycie intuicji bazującej na własnym lub obcym doświadczeniu. Większość parametrów jest ustalana manualnie i subiektywnie.

Na koniec wybiera się (znowu subiektywnie) ważny parametr lub kilka parametrów i już dla nich sprawdza się wszystkie kombinacje (tzw. Grid Search) wartości parametrów, zdefiniowane przez badacza. Ale często ten końcowy Grid Search jest nieefektywny, a manualny wybór parametrów na początku prowadzi do nieskutecznego lokalnego optimum. Badania pokazują, że nawet losowe sprawdzenie przestrzeni parametrów często prowadzi do lepszych wyników, niż wybór manualny [1].

3. Czym jest Hyperopt

HyperOpt jest open-source'ową biblioteką Pythona do optymalizacji bayesowskiej, stworzoną przez Jamesa Bergstrę. Została ona zaprojektowana do optymalizacji na dużą skalę dla modeli z setkami parametrów i pozwala na skalowanie procedury optymalizacji na wielu rdzeniach i wielu maszynach. Biblioteka ta jest wykorzystywana do optymalizacji procesów uczenia maszynowego, w tym przygotowania danych, wyboru modelu i jego hiperparametrów.

HyperOpt wymaga 4 zasadniczych komponentów do optymalizacji hiperparametrów: przestrzeni poszukiwań, funkcji straty, algorytmu optymalizacji oraz bazy danych do przechowywania historii. Przestrzeń poszukiwań to opis wszystkich parametrów, które będą optymalizowane oraz zakres ich możliwych wartości. Funkcja straty (lub funkcja wartości) to główna funkcja, która będzie optymalizowana.

Wejściem do funkcji są konkretne wartości parametrów, a wyjściem jest wartość straty. Najczęściej ciało funkcji zawiera przygotowanie danych (jeśli jest optymalizowane), definicję modelu ML, wytrenowanie go oraz obliczenie jego skuteczności. Wynikiem funkcji musi być pojedyncza wartość skalarna, która będzie minimalizowana. Jeśli wybrana metryka modelu ma być maksymalizowana, to niezbędne będzie jej przekształcenie (np. przemnożenie przez -1).

Algorytm optymalizacji to logika, która stoi za wyborem następnej kombinacji parametrów do symulacji. Najprostszą logiką jest losowy wybór parametrów. Bardziej zaawansowane algorytmy podejmują decyzję biorąc pod uwagę doświadczenie, czyli historię. Baza danych służy do przechowywania historii. Historia to obiekty, które muszą zawierać informację co do zbadanych kombinacji parametrów oraz wyniku funkcji strat. Najprostszą bazą danych jest obiekt klasy Trials z biblioteki hyperopt. Jest to domyślna baza, która przechowuje dane w pamięci komputera.

4. Instalacja oraz pierwszy prosty przykład

Zainstalować bibliotekę hyperopt można za pomocą polecenia:

pip install hyperopt

Poniższy przykład pokazuje jak zoptymalizować funkcję „eggholder”. Argumentami funkcji są dwa parametry, które są liczbami skalarnymi. Wynikiem funkcji jest pojedyncza wartość skalarna. Za hiperparametry będą uważane argumenty tej funkcji. Celem jest znalezienie argumentów funkcji, dla których wartość funkcji jest minimalna. 

Wzór na funkcję „eggholder”:

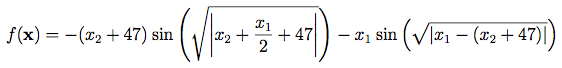
Przedstawione oraz porównane są dwa algorytmy doboru hiperparametrów do ewaluacji: drzewa estymatorów Parzena (ang. Tree of Parzen Estimators, TPE) oraz przeszukiwanie losowe (ang. random search). Główna różnica między tymi algorytmami jest taka, że algorytm przeszukiwania losowego działa zupełnie losowo i nie bierze pod uwagę doświadczenia. Algorytm TPE zaczyna przeszukiwanie identycznie - losowo, żeby nazbierać podstawową historię, a późniejsze propozycje są oparte o doświadczenie. 

Importowanie bibliotek

import numpy as np
 
from hyperopt import (
    hp,              # moduł posiadający różne rozkłady prawdopodobieństwa
    fmin,            # funkcja do minimalizacji
    Trials,          # baza danych historii
    tpe,             # algorytm drzewa estymatorów Parzena
    rand as hp_rand, # algorytm przeszukiwania losowego
)
 
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

definicja funkcji „eggholder”

def eggholder(x):  # x to dwuelementowa sekwencja
    return (-(x[1] + 47) * np.sin(np.sqrt(abs(x[0]/2 + (x[1]  + 47))))
            -x[0] * np.sin(np.sqrt(abs(x[0] - (x[1]  + 47)))))

Wizualizacja funkcji „eggholder”

x = np.arange(-512, 513)
y = np.arange(-512, 513)
xgrid, ygrid = np.meshgrid(x, y)
xy = np.stack([xgrid, ygrid])
 
fig = plt.figure(figsize=(20, 20))
ax = fig.add_subplot(111, projection='3d')
ax.view_init(45, -45)
ax.plot_surface(xgrid, ygrid, eggholder(xy), cmap='terrain')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('eggholder(x, y)')
plt.show()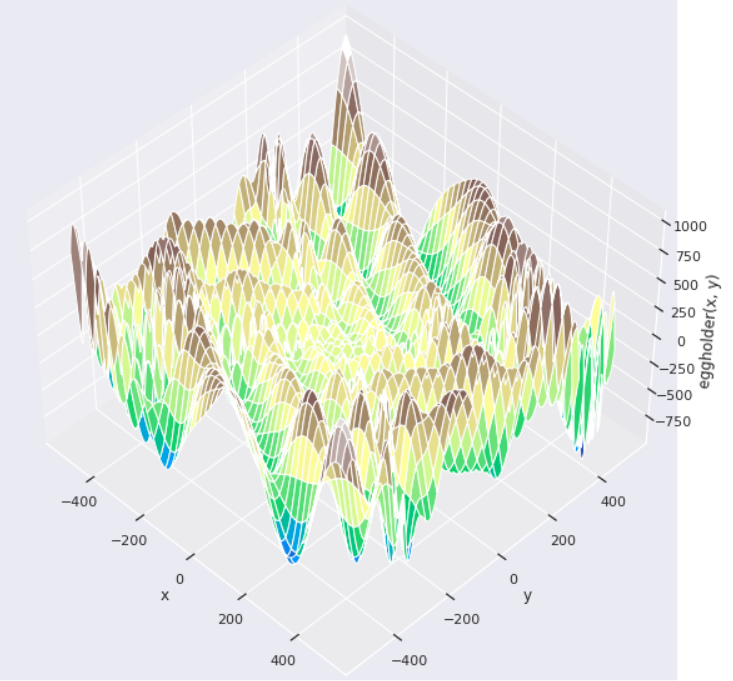

Globalny minimum funkcji na przedziale:

Definicja funkcji straty („objective”) oraz przestrzeni przeszukiwań. 

space = {
    'x1': hp.uniform('x1', -512, 512), # rozkład jednostajny na przedziale -512; 512
    'x2': hp.uniform('x2', -512, 512)
}
 
def objective(params):
    x1 = params['x1']
    x2 = params['x2']
    return eggholder((x1, x2))

Odpalenie funkcji minimalizującej z algorytmem TPE

trials_tpe = Trials()
best_tpe = fmin(objective, space, trials=trials_suggest, algo=tpe.suggest, max_evals=1000)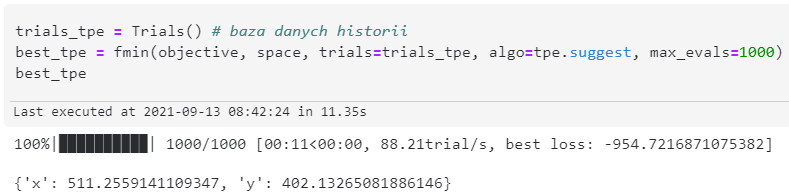

Odpalenie funkcji minimalizującej z algorytmem Random Search

trials_rnd = Trials()
best_rnd = fmin(objective, space, trials=trials_rnd, algo=hp_rand.suggest, max_evals=1000)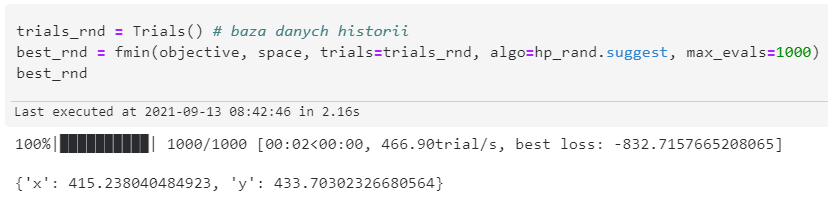

Z obiektu „trials” można uzyskać historię całego procesu optymalizacji. Poniżej znajduje się wykres średniej skumulowanej wyniku funkcji wartości względem numeru iteracji. Można zauważyć, że wartość algorytmu przeszukiwania losowego (RND) oscyluje wokół zera, wtedy jak średnia algorytmu TPE z czasem maleje.

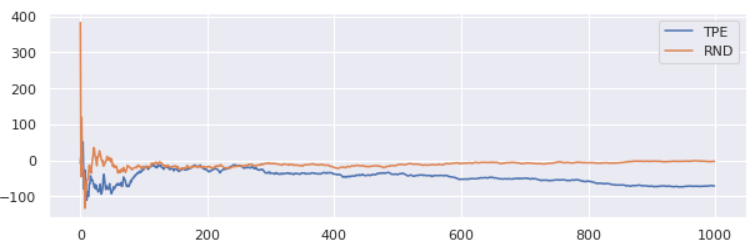
Następny wykres przedstawia parametry x1 oraz x2, które zostały zaproponowane przez każdy z algorytmów.

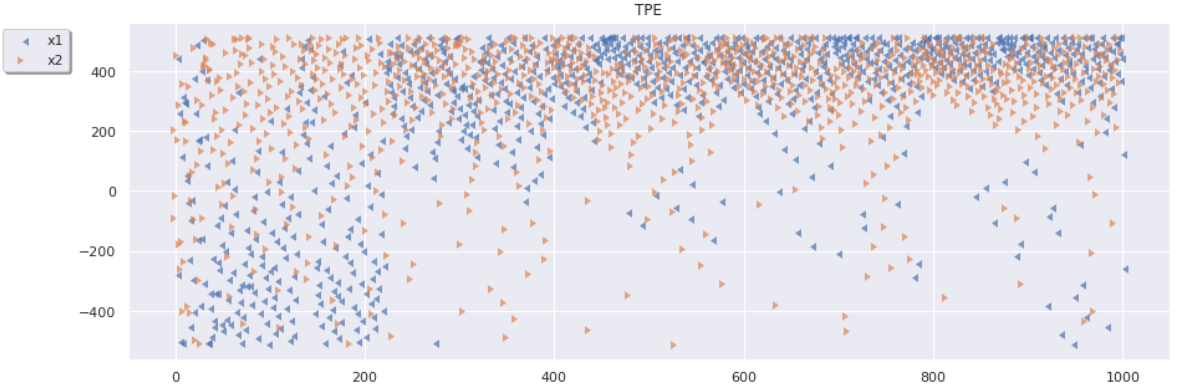
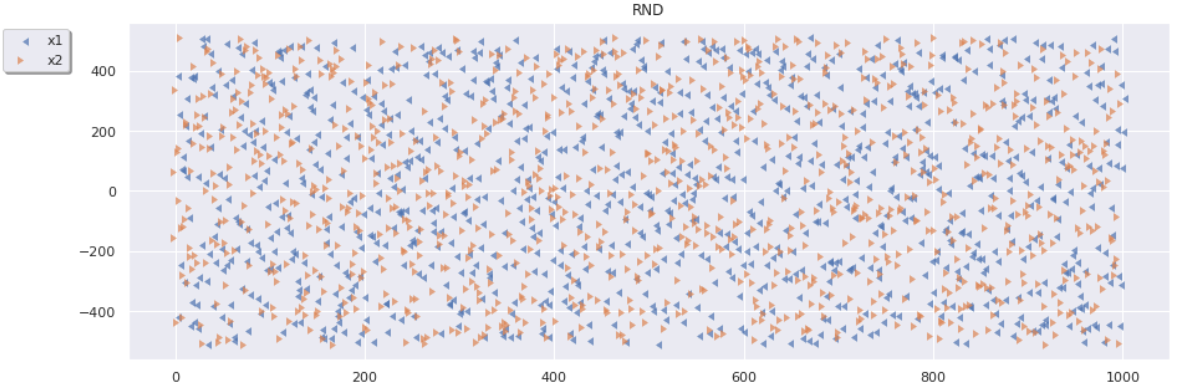
Z wykresu algorytmu losowego przeszukiwania (RND) można zauważyć, jak przez cały okres przeszukiwania przestrzeń była eksplorowana. Brak jakichkolwiek wzorców. Wykres algorytmu TPE wygląda zupełnie inaczej.

Na samym początku przez pierwsze kilkadziesiąt iteracji przestrzeń jest eksplorowana w celu zgromadzenia podstawowej historii. Do około 225 iteracji algorytm eksploatował wartości bliżej minimalnej dla zmiennej x1 oraz wartości bliżej maksymalnej dla zmiennej x2. A następnie dla obu zmiennych były eksploatowane wartości bliżej maksymalnej, gdzie i znajduje się minimum globalne. Jest to wizualne przedstawienie tego, że algorytm TPE eksploatuje przestrzeń, w odróżnieniu od algorytmu Random Search. Na ogół algorytm TPE dostarcza wyniki lepsze niż Random Search.

Każdy z algorytmów po 1000 iteracjach osiągnął wartość bliską do minimum globalnego. Warto zaznaczyć, że wyniki hyperopt domyślne są niedeterministyczne, co oznacza, że każde odpalenie optymalizatora może dać inne wyniki.

Podsumowanie

Gratulacje, dotarłeś do końca tego artykułu! W nim dowiedziałaś/-łeś się, czym jest HyperOpt, jaki jest jego cel, jak działa i jakie są jego główne komponenty.

W skrócie: HyperOpt jest narzędziem dla optymalizacji hiperparametrów, zarówno w specyficznych funkcjach, jak i w optymalizacji potoków (ang. pipeline) uczenia maszynowego. Jedną z wielkich zalet HyperOpt jest zaimplementowana optymalizacja bayesowska ze specyficznymi adaptacjami, co czyni HyperOpt narzędziem, które warto rozważyć przy dostrajaniu hiperparametrów.

Jeśli uważasz, że to narzędzie okaże się przydatne w twojej pracy, to więcej szczegółów można znaleźć w podanych niżej linkach. Jest tam m.in. link do oficjalnej dokumentacji oraz oryginalna praca napisana przez autora biblioteki.

Pozdrawiam i do zobaczenia.

Linki

[1] J. Bergstra and Y. Bengio. Random Search for Hyperparameter Optimization J. Machine Learning Research, 13:281--305, 2012. Link: https://www.jmlr.org/papers/volume13/bergstra12a/bergstra12a 
[2] https://github.com/hyperopt/hyperopt/wiki/FMin
[3] https://github.com/hyperopt/hyperopt
[4] http://hyperopt.github.io/hyperopt/