Czym jest deep learning i sieci neuronowe
Poznaj historię uczenia maszynowego, różnice między machine i deep learningiem oraz sprawdź, jak zbudować prostą sieć neuronową.
Pisząc ten artykuł, mam nadzieję zapoczątkować pewien cykl o stale zyskujących popularność i nowych zastosowaniach sieci neuronowych. Zanim jednak przejdziemy do praktycznych zastosowań, poznajmy nieco teorii. O historii rozwoju uczenia głębokiego, podstawowych zastosowaniach oraz budowie sieci neuronowej przeczytacie w dalszej części artykułu.
Historia sieci neuronowych
Początki sieci neuronowych sięgają lat 40. XX wieku, kiedy to opracowano model neuronu, który potrafił rozpoznawać jedynie dwie kategorie obiektów, na podstawie wag zadanych przez operatora. Dopiero pod koniec lat 50. dalszy rozwój tej dziedziny zaowocował zbudowaniem pierwszej sieci neuronowej zwanej perceptronem, której zadaniem było rozpoznawanie znaków. Po pierwszej fali zainteresowania nastąpił okres stagnacji i krytycyzmu, który trwał do czasu wprowadzenia algorytmu wstecznej propagacji błędów w 1986r.
Niestety kolejna faza entuzjazmu została dość szybko wygaszona ze względu na ograniczenia ówcześnie istniejącej technologii komputerowej. Do implementacji sieci zdolnej wykonać minimalnie złożone obliczenia, potrzeba było bardzo dużo czasu (tygodnie, miesiące, a nawet lata obliczeń). Ostatni przełom nastąpił w 2006r., wraz z rozwojem technologii komputerowej i Big Data, który trwa po dziś dzień. W tym czasie opracowane zostały sieci głębokie z efektywnymi metodami ich uczenia. Niemały udział w nim miało pojawienie się kart graficznych z tysiącami rdzeni, które znacząco skróciły czas uczenia.
Uczenie głębokie vs uczenie maszynowe
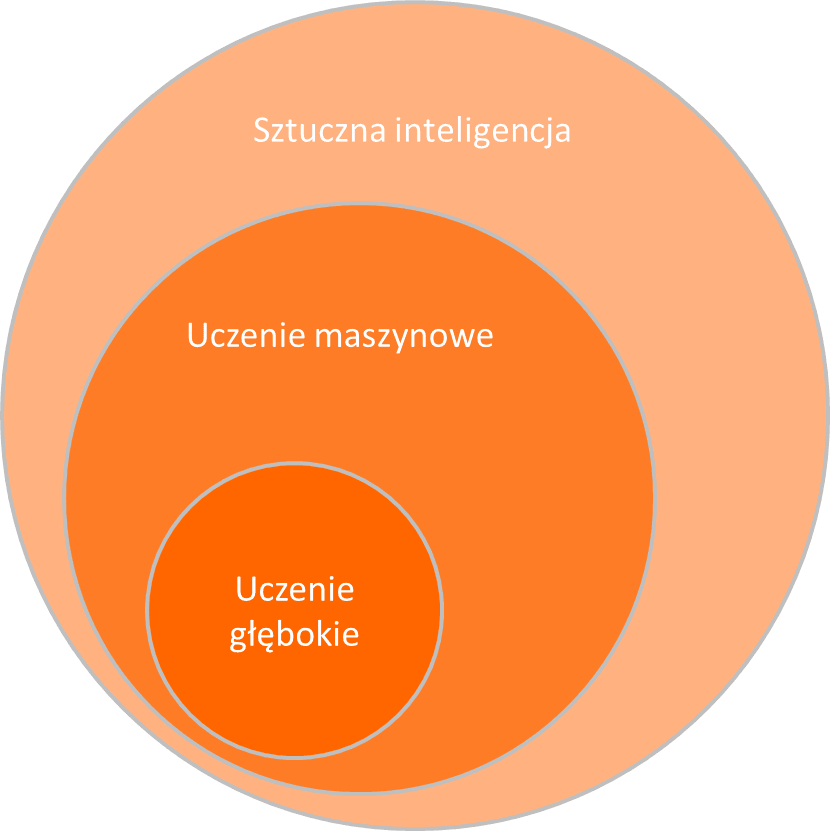
Jak możemy zobaczyć na powyższym diagramie, uczenie głębokie jest poddziedziną uczenia maszynowego. Podstawowym czynnikiem wyróżniającym deep learning jest to, że proces uczenia nie wymaga kontroli człowieka, czyli zachodzi w sposób nienadzorowany.
Ze względu na elastyczność technik uczenia głębokiego i różnorodność struktur sieci neuronowych, uczenie głębokie ma najszersze zastosowanie spośród technik uczenia maszynowego i może z powodzeniem rozwiązywać problemy, do których dotychczas aplikowane były klasyczne metody. W tym miejscu należałoby jednak rozważyć, czy potencjalne korzyści z zastąpienia oraz dłuższy czas nauki modelu, rekompensują koszty.

Modele sieci neuronowych nie sprawdzą się też w sytuacji, w której potrzebna jest interpretowalność wyniku. Nie występuje tutaj mechanizm obliczania istotności cech, który tłumaczy na ile dana cecha oddziałuje na zmienną objaśnianą. Ze względu na duży poziom generalizacji zmiennych wejściowych, jest to swego rodzaju black box, który zwraca aproksymowany wynik.
Zastosowania sieci neuronowych
Ze względu na swoją uniwersalność, sieci neuronowe mają wiele zastosowań praktycznych (w niedalekiej przyszłości zapewne powstanie ich jeszcze więcej). Ich zastosowanie można podzielić na następujące kategorie:
- klasyfikacja (np. mowy, obrazów, tekstu);
- regresja;
- rozpoznawanie (np. obiektów na obrazie);
- identyfikacja (np. konkretnych osób na podstawie obrazu/głosu);
- prognozowanie (np. szeregów czasów, kursów walut);
- odtwarzanie z redukcją zniekształceń w danych wejściowych;
- transkrypcja mowy na tekst;
… oraz wiele innych zagadnień, gdzie dobór klasycznych metod jest zbyt skomplikowany, bądź wszędzie tam, gdzie nie wymagane są odpowiedzi ilościowe tylko jakościowe.
Budowa sieci neuronowej
Podstawową jednostką sieci neuronowej jest, jak wskazuje sama nazwa, neuron. Neuron jest prostym elementem obliczeniowym, do którego doprowadzane są sygnały z wejść sieci lub neuronów poprzedniej warstwy. Każdy sygnał (zmienna wejściowa) mnożony jest przez odpowiadającą mu wagę (wagi są zmieniane w trakcie procesu uczenia). Waga może przyjmować wartość dodatnią, tzw. pobudzającą, ujemną tzw. opóźniającą lub równą 0, jeśli nie ma połączeń między neuronami. Następnie zważona suma cech wejściowych przekazywana jest jako argument do funkcji aktywacji.
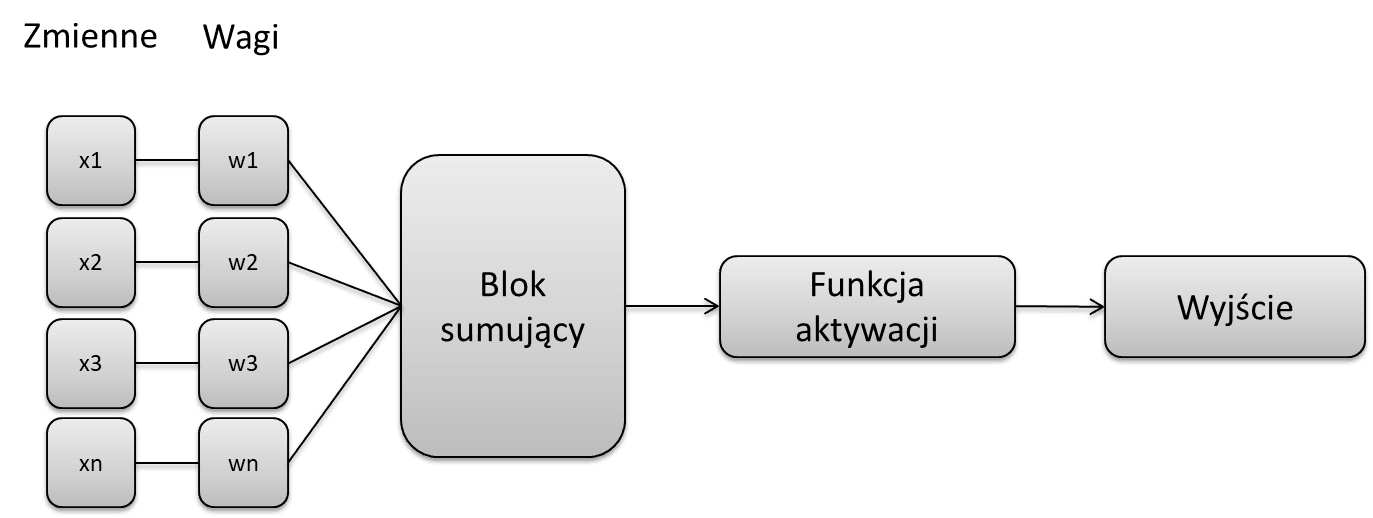
Model neuronu
Wartość funkcji aktywacji jest wartością wyjściową danego neuronu i przekazywana jest do neuronów na następnej warstwie. Funkcja aktywacji przyjmuję jedną z trzech postaci:
- nieliniowa;
- liniowa;
- skoku jednostkowego.
Wybór funkcji zależy od rodzaju problemu, jaki zadajemy sieci do rozwiązania. Najczęściej stosowane są funkcje nieliniowe ze względu na to, że neurony o takich charakterystykach wykazują największe zdolności do nauki i umożliwiają w sposób płynny odwzorowanie zależności między cechą wejściową i wyjściową. Dzięki temu na wyjściu uzyskujemy wartość ciągłą zamiast logicznej (Prawda lub Fałsz).
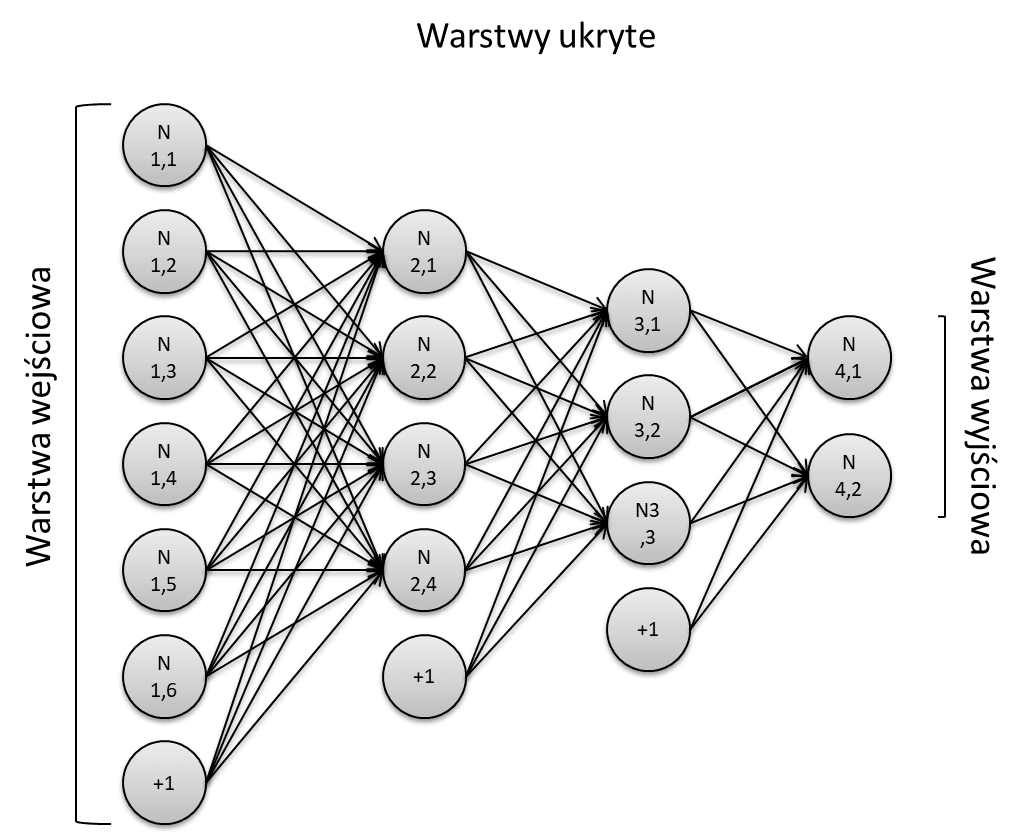
Architektura jednokierunkowej sieci wielowarstwowej
Najczęściej spotykanym rodzajem sieci jest sieć wielowarstwowa, w której neurony grupowane są w warstwy. Jej cechą charakterystyczną jest posiadanie przynajmniej jednej warstwy ukrytej, pośredniczącej w komunikacji między danymi na wejściu i wyjściu. W ramach jednej warstwy neurony nie komunikują się między sobą, natomiast pomiędzy warstwami obowiązuje zasada „każdy z każdym”. Na jednej warstwie mogą się znajdować tylko neurony tego samego typu.
Wyróżniamy trzy typy warstw:
- warstwa wejściowa – jej jedyną funkcją jest pobieranie danych i przekazywanie ich do pierwszej warstwy ukrytej. Liczba neuronów z reguły odpowiada liczbie cech przekazywanego zbioru;
- warstwa ukryta – warstwa odpowiedzialna za naukę i wykonywanie obliczeń, nie można do niej w sposób bezpośredni przekazywać informacji;
- warstwa wyjściowa – warstwa obliczająca wartości wyjściowe całej sieci i zwracająca je na zewnątrz.
Każda warstwa, poza wyjściową, jest doposażona w stałą wartość przesunięcia nazywaną bias. Bias jest dodatkowym neuronem przechowującym wartość 1. W architekturze sieci neuronowej zwyczajowo oznaczany jest jako „+1” i nie posiada relacji z warstwami poprzedzającymi, pomimo tego jego waga również jest modyfikowana w trakcie procesu uczenia. Mówiąc najprościej bias jest niezależnym czynnikiem, którym pozwala lepiej dopasowywać się sieci do oczekiwanego rezultatu.
Najtrudniejszym etapem budowy sieci jest określenie liczby warstw z liczbą neuronów. Dla sieci wielowarstwowych przydatna jest metoda piramidy geometrycznej, która zakłada, że liczba neuronów w kolejnych warstwach tworzy kształt piramidy i maleje od wejścia do wyjścia, jest to jednak jedynie metoda przybliżona. Generalnie uczenie rozpoczyna się z małą liczbą warstw i neuronów ukrytych i doświadczalnie zwiększa się ich liczbę, obserwując postępy procesu. Jeśli sieć będzie miała zbyt mało neuronów, to nie będzie w stanie poprawnie się uczyć czy realizować skomplikowanych procesów. Z drugiej strony zbyt duża liczba neuronów będzie prowadziła do znacznego wydłużenia czasu liczenia, jak i bardzo często do przeuczenia.
Prosta sieć neuronowa w Keras
Skoro już znamy nieco teorii, przejdźmy do kwestii praktycznych. Zobaczmy, jak zbudować bardzo prostą sieć w Pythonie z wykorzystaniem biblioteki keras, rozwijanej przez Google w ramach pakietu tensorflow. Do tego celu utworzymy zbiór losowo generowanych liczb i przygotujemy model sieci neuronowej, której zadaniem będzie klasyfikacja binarna.
import numpy as np
from tensorflow import keras
from matplotlib import pyplot as plt
data = np.random.random((1000, 10))
labels = np.where(np.random.random((1000))>.5,1,0)
W pierwszej kolejności zaimportujmy potrzebne nam pakiety i wygenerujmy zbiór testowy. Na potrzeby prezentacji niech to będzie zbiór o wymiarze 1000 wierszy na 10 kolumn z losowo dopisanymi etykietami: 1 – dla wartości powyżej 0.5, 0 – dla wartości mniejszych równych 0.5.
W keras istnieją dwie metody deklaracji sieci: sekwencyjna i funkcyjna. Omówimy obydwie.
Deklaracja sekwencyjna pozwala na tworzenie modelu warstwa po warstwie. Takie podejście sprawdza się w większości przypadków, ma jednak pewne ograniczenia. Np. nie zezwala na tworzenie modeli posiadających współdzielone warstwy, bądź posiadających więcej niż jedną warstwę wejściową/wyjściową. Nie wymaga też jawnej deklaracji warstwy wejściowej, ponieważ taką rolę pełni zawsze pierwsza warstwa dodana do modelu.
model = keras.models.Sequential()
model.add(keras.layers.Dense(7, activation=keras.activations.relu, input_shape=(10,)))
model.add(keras.layers.Dense(5, activation=keras.activations.relu))
model.add(keras.layers.Dense(3, activation=keras.activations.relu))
model.add(keras.layers.Dense(1, activation=keras.activations.sigmoid))
model.summary()
Po uruchomieniu wbudowanej funkcji summary, możemy zobaczyć, jak wygląda architektura stworzonej przez nas sieci.
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 7) 77
_________________________________________________________________
dense_1 (Dense) (None, 5) 40
_________________________________________________________________
dense_2 (Dense) (None, 3) 18
_________________________________________________________________
dense_3 (Dense) (None, 1) 4
=================================================================
Total params: 139
Trainable params: 139
Non-trainable params: 0
Struktura funkcjonalna jest znacznie bardziej elastyczna i pozwala definiować modele o znacznie bardziej złożonej architekturze, z większą ilością warstw wejściowych/wyjściowych, a także współdzielące ze sobą poszczególne warstwy. Model jest definiowany poprzez utworzenie instancji warstw i łączenie ich ze sobą.
input_tensor = keras.layers.Input(shape=(10,))
x1 = keras.layers.Dense(7, activation='relu')(input_tensor)
x2 = keras.layers.Dense(5, activation='relu')(x1)
x3 = keras.layers.Dense(3, activation='relu')(x2)
output_tensor = keras.layers.Dense(1, activation='sigmoid')(x3)
model = keras.models.Model(inputs=input_tensor, outputs=output_tensor)
model.summary()
Po wyświetleniu podsumowania możemy zobaczyć, że architektura sieci stworzonej w ten sposób niczym nie różni się od podejścia sekwencyjnego, poza jawnym wskazaniem warstwy wejściowej.
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 10)] 0
_________________________________________________________________
dense_4 (Dense) (None, 7) 77
_________________________________________________________________
dense_5 (Dense) (None, 5) 40
_________________________________________________________________
dense_6 (Dense) (None, 3) 18
_________________________________________________________________
dense_7 (Dense) (None, 1) 4
=================================================================
Total params: 139
Trainable params: 139
Non-trainable params: 0
Kolejnym krokiem jest kompilacja modelu. Na tym etapie dobieramy optymalizator sieci, funkcję straty i miernik jakości. W tym artykule nie będę się skupiał na poszczególnych optymalizatorach. Warto wiedzieć, że najczęściej stosowanym i najbardziej efektywnym dla większości zastosowań jest ADAM (Adaptive Moment Estimation).
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
Na koniec przechodzimy do sedna problemu, czyli do uczenia sieci. Proces uczenia wywołujemy metodą fit, która przyjmuje dwa podstawowe parametry (poza zbiorem danych i etykiet): batch_size i epochs. Parametr batch_size definiuję liczbę próbek, które musi przejść sieć przed aktualizacją wewnętrznych parametrów. W ogólnym rozumieniu jest to pętla, w której dokonywane są prognozy porównywane z oczekiwanymi zmiennymi wyjściowymi. Na końcu pętli obliczany jest błąd, który służy sieci do ulepszania modelu.
Parametr epochs definiuje ile razy algorytm uczenia będzie działał na pełnym zestawie danych. Jeden epoch oznacza, że każda próbka w zbiorze danych treningowych będzie miała okazję zaktualizować parametry modelu wewnętrznego. Epoch składa się z jednej lub więcej partii. W naszym przykładzie algorytm uczenia przetworzy w całości zbiór wejściowy 10 razy i co każde 16 próbek dokona aktualizacji parametrów wewnętrznych modelu.
history = model.fit(data, labels, batch_size=16, epochs=10, validation_split=.2)
W trakcie uczenia algorytm zwraca wyniki co każdą pełną iterację, (epoch) dzięki temu możemy dokonać oceny procesu uczenia oraz porównać je ze zbiorem walidacyjnym (jeżeli został wskazany). Jak widać na naszym przykładzie, trafność na zbiorze testowym stale rosła, co pokazuje, że w trakcie każdej iteracji sieć była w stanie poprawiać swoje wyniki i dopasowywać się do oczekiwanego na wyjściu wyniku. Natomiast na zbiorze walidacyjnym widzimy wahania miernika jakości. Pokazuje to jakość modelu na niezależnym zbiorze oraz ułatwia podjęcie decyzji do co zakończenia nauki modelu lub nawet zmiany architektury sieci.
fig, ax = plt.subplots()
ax.plot(range(1,11), history.history['accuracy'], label='Train Accuracy')
ax.plot(range(1,11), history.history['val_accuracy'], label='Validation Accuracy')
ax.legend(loc='best')
ax.set(xlabel='epochs', ylabel='accuracy')Podsumowanie
Jak widać, praca z sieciami neuronowymi nie jest taka skomplikowana, jak mogłoby wskazywać samo zagadnienie. Dzięki ogromnemu zaangażowaniu środowiska naukowego i open source, można przygotować proste modele uczące z jedynie odrobiną znajomości programowania.

